○発表者：
中島　蒼　（東京大学 大学院情報理工学系研究科　博士課程3年）
小林　徹也（東京大学 生産技術研究所　准教授）

○発表のポイント：
◆進化と学習の関係を扱う新たな数理手法を構築することで、先祖の経験を生物個体が学習し、先祖をまねた形質を選択すると仮定すると、ランダムな突然変異のみを考慮した場合よりも、進化が加速されることを数理的に明らかにした。
◆学習による進化の加速を定量化する方法として、フィッシャーの基本定理を拡張した。
◆これらの理論は、生体における学習と進化の関係の理解のみならず、学習と進化を組み合わせた工学・情報システムの開発にも寄与すると期待される。

○発表概要：
　自然選択による進化により、多様な形質を持つ生物の集団は環境に適応していく。従来の進化学では、集団内の形質の多様性はランダムな突然変異で生じ、親世代の経験は反映されないと考えられてきた。しかしながらエピジェネティックス（注１）研究の発展などにより、親世代の経験に依存した突然変異が起きる可能性が近年示唆され始めた。つまり、先祖の経験を各個体が学習し、多様性にバイアスをもたらす可能性である。しかし、これにより進化がどれだけ加速しうるのかなどを扱う体系的な理論は存在していない。
　東京大学 大学院情報理工学系研究科 博士課程３年の中島 蒼 大学院生と同 生産技術研究所の小林 徹也 准教授は、理論進化学の数理手法を基盤に、学習と進化の関係を考察する数理的な枠組みを構築した。まず先祖の形質をまねる先祖学習が、適応度（注２）の勾配、つまりどういう方向に形質を変化させると適応度が大きく上昇するかを経験から推定することと等価であり、その結果進化が加速されることを明らかにした。またフィッシャーの自然選択の基本定理として知られる進化速度を測る定理（注３）を拡張し、学習が進化をどの程度加速するかを定量的に予言する関係式も与えた。これらは、親子で相関を示す実験データの解釈や、先祖学習を検証する新たな実験系の設計に加え、遺伝的アルゴリズム（注４）や機械学習などへの応用など、理学・工学の双方での応用が期待できる数理的基礎になることが期待される。
　本研究成果は２０２２年１月３１日に American Physical Society による「Physical Review Research」に掲載された。

○発表内容：
＜研究背景＞
　自然選択による進化は、多様な形質を持つ生物集団の中から環境により適したものがより多くの子孫を残すことで、集団全体として環境に適応していくというメカニズムである。集団内の形質の多様性は、次世代が生み出される際の突然変異により維持されている。従来の進化学では、突然変異は親世代の経験とは無関係でランダムなものと考えられてきた。これは親世代の経験を次世代に遺伝的に継承することはないというダーウィン進化の前提による。しかし近年、非遺伝的な形で親世代の経験が継承される可能性として、エピジェネティックな状態や文化などが考えられ始めている。このように親世代の経験に依存した変異が生じる、すなわち先祖の経験からの学習を各個体が行うと、突然変異のみの場合より進化が加速され、より早く環境に適応できると考えられる。しかしながら学習と進化の関係はこれまで十分検討されてこなかった。

＜研究内容＞
　東京大学 大学院情報理工学系研究科 博士課程３年の中島 蒼 大学院生と同 生産技術研究所の小林 徹也 准教授は、理論進化学の数理手法であるフィッシャーの自然選択の基本定理などを発展させることで学習と進化の関係を考察する数理的な枠組みを構築した。

１．先祖の経験は進化を加速する
　本研究では、個体群動態（注５）と呼ばれる数理モデルを用いて、先祖の経験を用いた学習により集団の進化が加速されるかを検討した。進化の早さを見る対象として生物個体の形質変化を取り扱った。個体の形質には親世代からの継承のみでは決まらないゆらぎや個体差がある。そこで我々は、個体が結果的にある形質をとる確率（以下「形質発現戦略」と呼ぶ）が世代間で継承され、また学習により変化する状況を考えた。また学習の方法として、親と似た非継承的な個体差を持つ確率を高くなるよう形質発現戦略が変化するという、先祖をまねる先祖学習を考えた。これは「先祖が発現し生き残った形質は自身の生存にも寄与するはずである」という生存バイアスを活用した学習法である。
　まずは数値実験により先祖学習により進化が加速されることを確認した（図２）。先祖学習を行う生物集団の増殖をシミュレーションし、(１) 最適な形質発現戦略が獲得されること；(２)獲得の早さはランダムな変異のみのときと比べ早いことを確認した。加えて個体群動態の数理手法である経路積分表示や変分表現（注６）を活用することで先祖学習は集団適応度の勾配を推定して進化を勾配法（注７）と同じ原理で加速していることを明らかにし、先祖学習は進化を質的に加速すると結論付けた。さらにこの結果は集団内の他の個体間とのコミュニケーションがない、並列的な学習でも進化は加速されることも示している。

２．進化の加速の定量化を与えるフィッシャーの基本定理の拡張
　先祖学習により進化がどれくらい加速されるかを定量化することは、どのような環境や状況において学習が有利になるかを考察する上で重要である。また定量的な予言を行うことは、本研究の結果を実験的に検証するためにも必要である。
　本研究では進化の加速を定量化するため、理論進化学のフィッシャーの基本定理（fundamental theorem of natural selection)（注３）を先祖学習に拡張した。本研究はこの定理を先祖学習に拡張し、先祖学習による集団適応度の増分は形質発現戦略の個体適応度の分散で特徴づけられることを証明した。この定理は学習の頻度と学習の早さのトレードオフ関係を与える点でも重要である。

＜今後の予定＞
　個体の情報処理と進化の関係は多くの研究者の興味を惹き研究されてきたテーマであり、生物がなぜ情報処理をする仕組みを持ち発展させてきたかの解明に寄与するものである。拡張されたフィッシャーの基本定理は定量的な予言を与えているため、親子相関があるデータの解釈や先祖学習を検証する新たな実験系の設計に使えるものである。加えて生物の進化は遺伝的アルゴリズムや粒子フィルタなどの形で情報学のアルゴリズムの設計にも応用されており、本研究は工学な応用も考えられる。本研究をこれらの方向性で進展させることは、理学・工学の双方において意義があるものと期待される。

※本研究は日本学術振興会科学研究費助成事業（JP19J22607, 19H05799, 19H03216）、JST ACT-X (JPMJAX190L), CREST（JPMJCR1927, JPMJCR2011）などの助成や支援を受けて行われた。

○発表雑誌：　
雑誌名：「Physical Review Research」（１月３１日）
論文タイトル：Acceleration of Evolutionary Processes by Learning and Extended Fisher's Fundamental Theorem
著者：So Nakashima*, Tetsuya J. Kobayashi
DOI番号：10.1103/PhysRevResearch.4.013069

○問い合わせ先：　
東京大学 生産技術研究所
准教授　小林 徹也（こばやし てつや）
Tel：03-5452-6798　　Fax：03-5452-6798
E-mail：tetsuya（末尾に"@sat.t.u-tokyo.ac.jp"をつけてください）
URL：https://research.crmind.net/index_jp.html

○用語解説：
（注１) エピジェネティックス
　DNAの塩基配列以外の形で次世代に形質が継承される仕組みを研究する学問分野である。そのような仕組みの例としてはDNAのメチル化やヒストンの修飾などが知られている。

（注２) 集団適応度
　生物集団が増殖する早さを測る指標の１つであり、個体数の対数の増分の時間平均として定義される。個体数の指数的な振る舞いを概観できる点で有用な量であり、個体群動態の研究でよく用いられる。

（注３）フィッシャーの基本定理
　従来の学習のない自然選択による進化で適応度が上昇していく早さを定量化する定理である。自然選択による平均適応度の増分は適応度の分散に比例するという定量的な関係を与えている。

（注４）遺伝的アルゴリズム
　自然選択による進化を数理最適化に応用したアルゴリズムである。目的関数を最大化する引数を探索するため、それぞれが解の候補に対応する仮想的な個体の進化をシミュレーションする。目的関数の値がより大きい解に対応する個体がより多くの子孫を残す仮想的な状況を設定しシミュレーションを行うことで、最終的に目的関数の値が大きい解に対応した個体の集団が得られる。

（注５）個体群動態
　生物集団の個体数の変化を微分方程式などで記述した数理モデル。分枝過程やロジスティック写像など様々なものがあるが、本研究では分枝過程を基にした決定論的なモデルを用いている。

（注６）経路積分表示と変分表現
　集団適応度を解析的に計算するために用いられる数理手法である。自分とその先祖の形質の履歴（経路）全体を用いた変分問題の解として集団適応度を特徴づけている。

（注７）勾配法
　数理最適化において目的関数の値が大きくなる引数を探索するのに用いられる手法である。関数の勾配方向に解の更新するのを逐次的に繰り返すことで関数の極大値を発見できる。

○添付資料：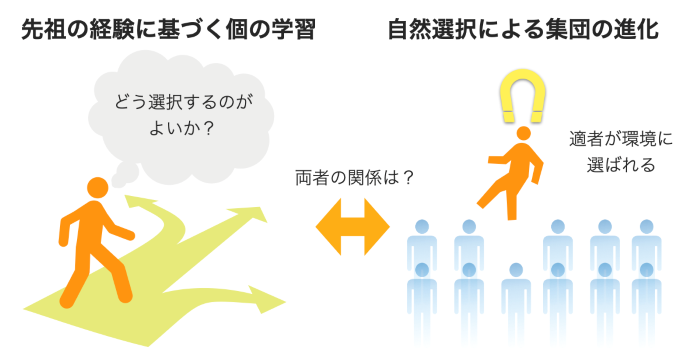

図１　先祖の経験からの学習と自然選択による集団進化を対比した概念図。

図２　先祖学習が進化を加速することの数値実験。先祖学習・突然変異それぞれでの系譜（親子関係）を示している。各個体の色が集団適応度を示しており、値が大きいほど適応度が高い。先祖学習を行うと進化が早いことが分かる。