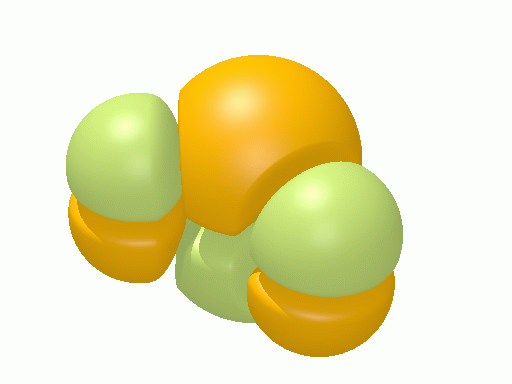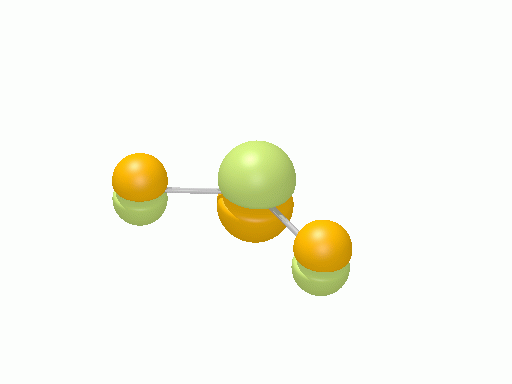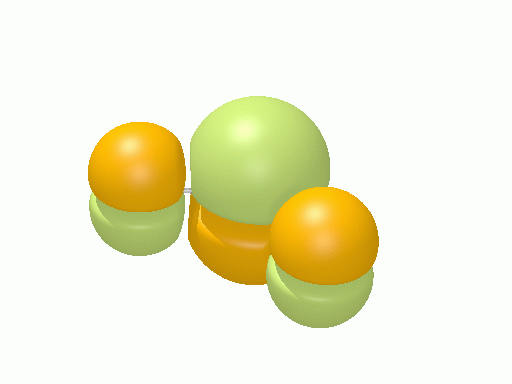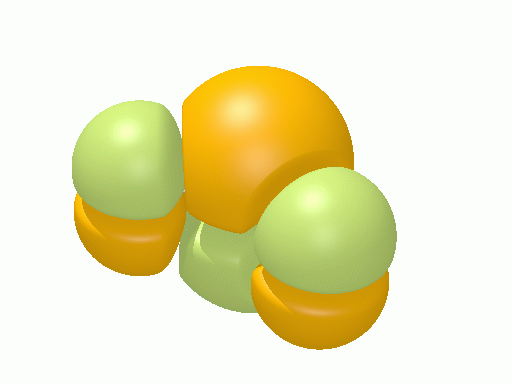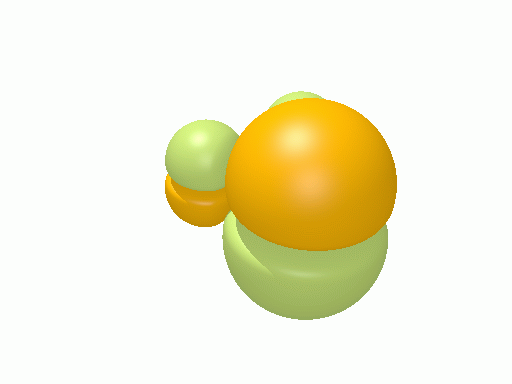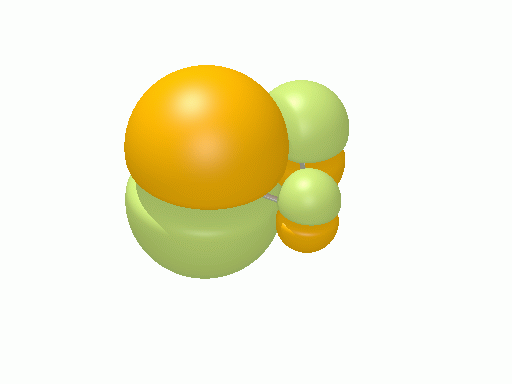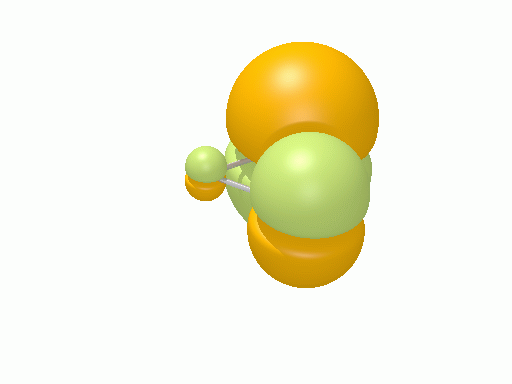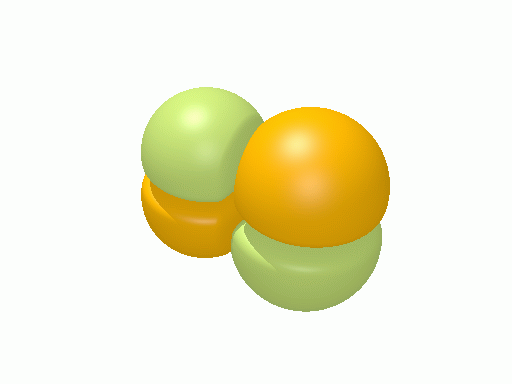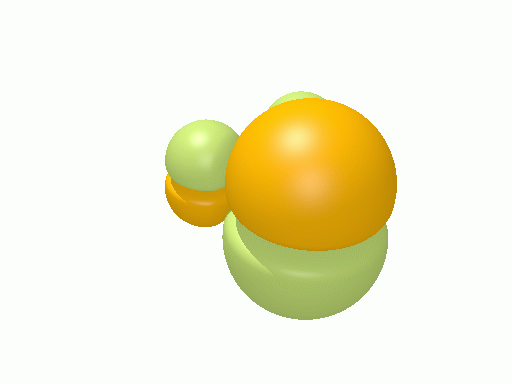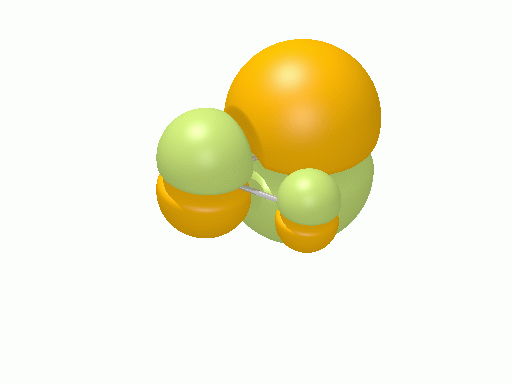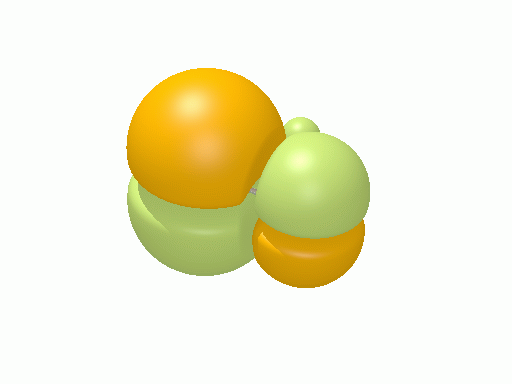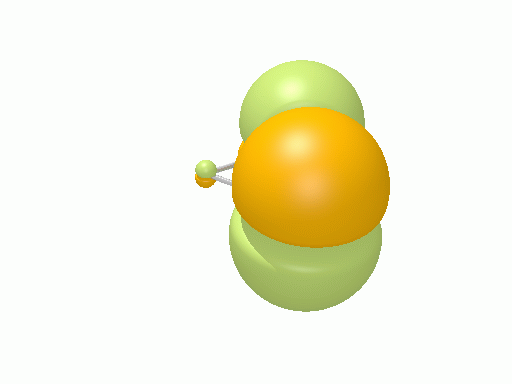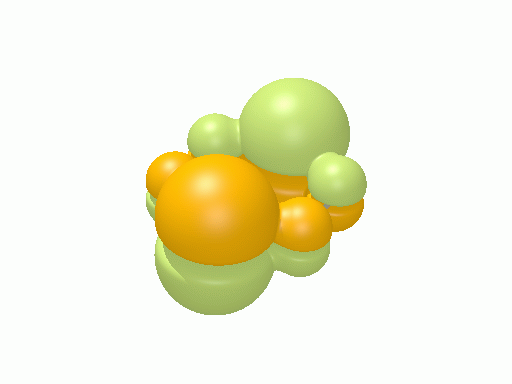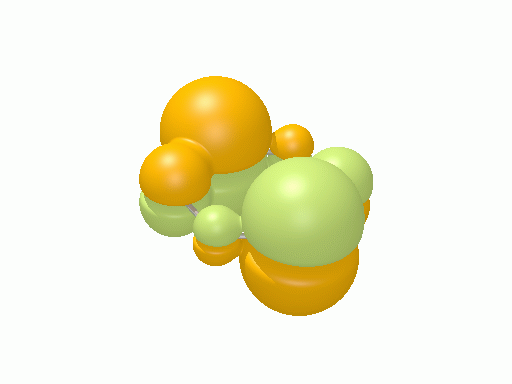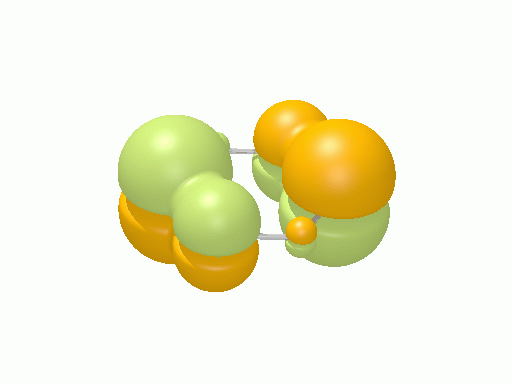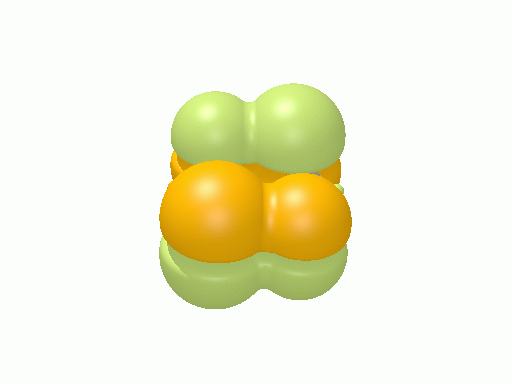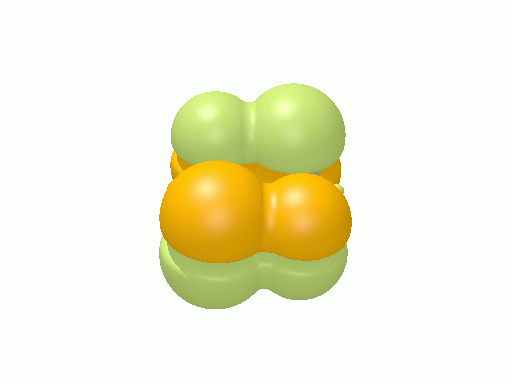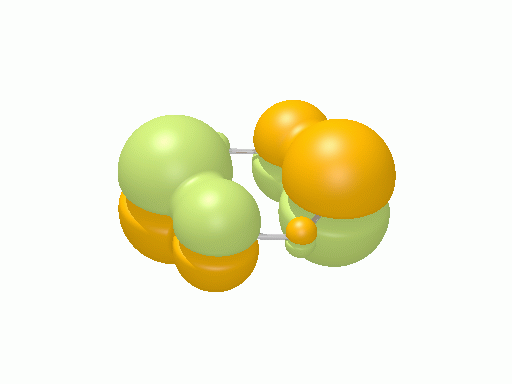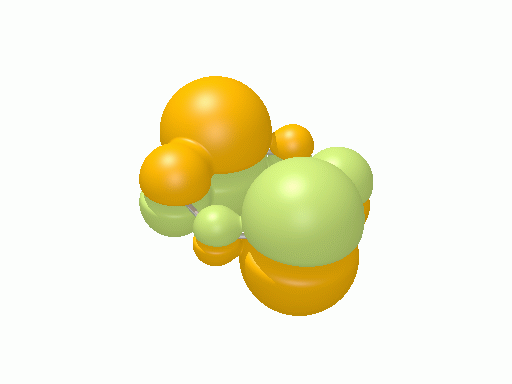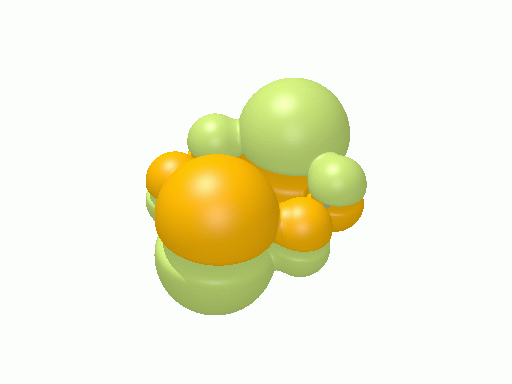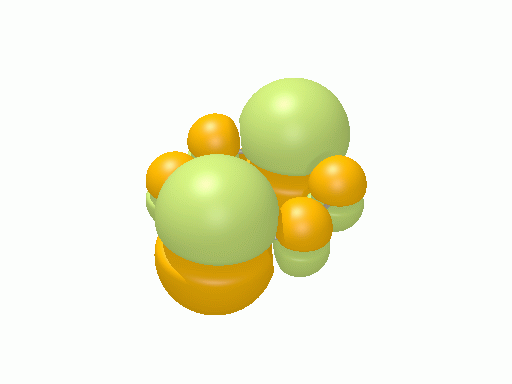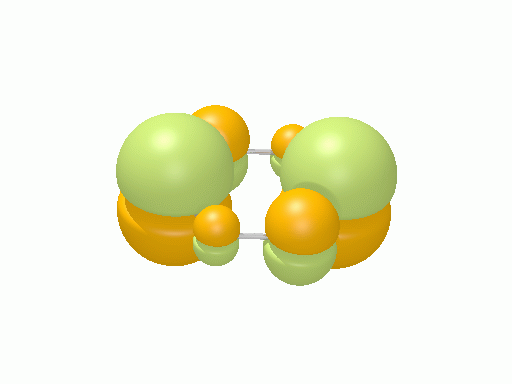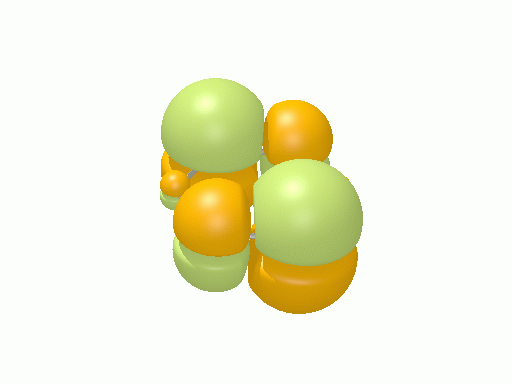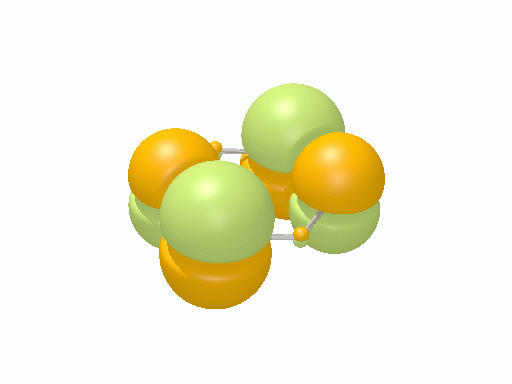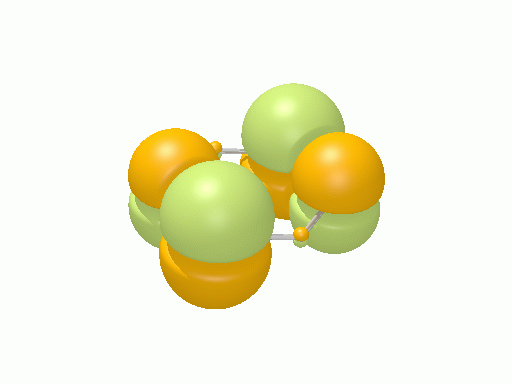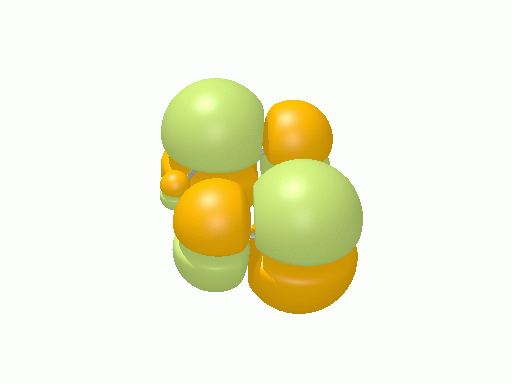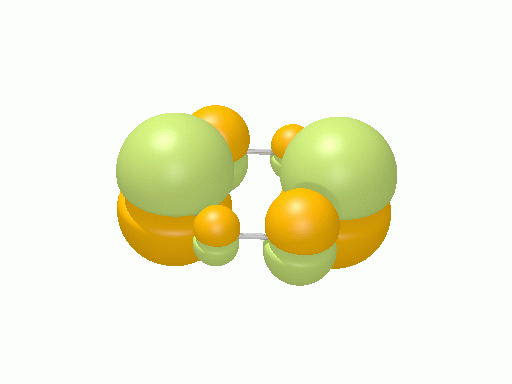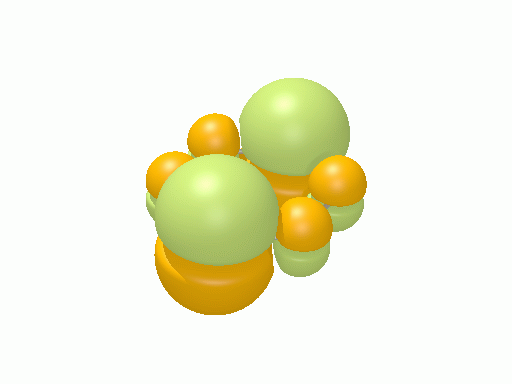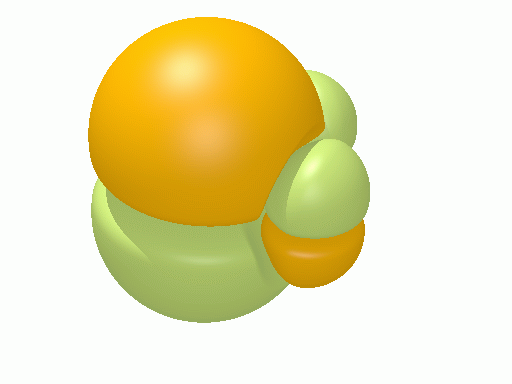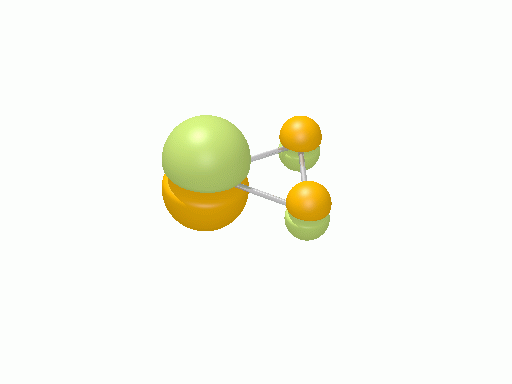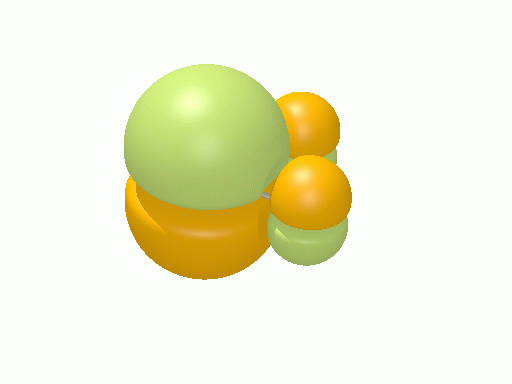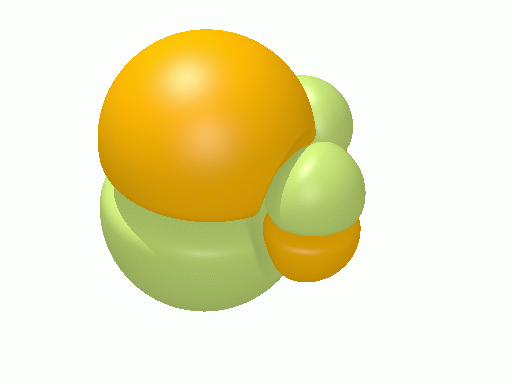Houjou Lab. - IIS, Univ. Tokyo

分子軌道 †

複素波動関数 †

シュレーディンガー方程式

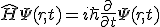
$\hat{H}\Psi(r,t)=i\hbar\frac{\partial}{\partial t}\Psi(r,t)$

において、解の波動関数を変数分離する。

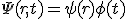
$\Psi(r,t)=\psi(r)\phi(t)$

これを方程式に代入すれば、Eを固有値として、

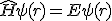
$\hat{H}\psi(r)=E\psi(r)$

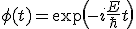
$\phi(t)=\exp\(-i\frac{E}{\hbar}t\)$

という関係が得られる。つまり波動関数は、空間部分の軌道関数と時間に依存する位相因子の積で表される。

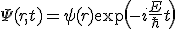
$\Psi(r,t)=\psi(r)\exp\(-i\frac{E}{\hbar}t\)$

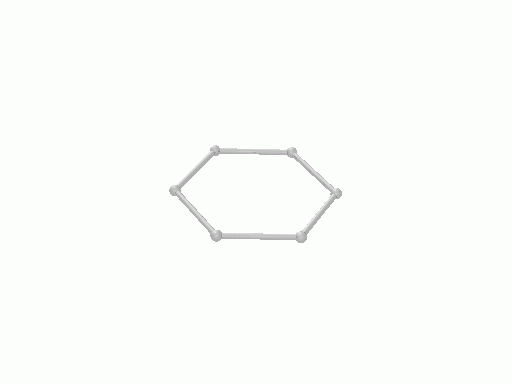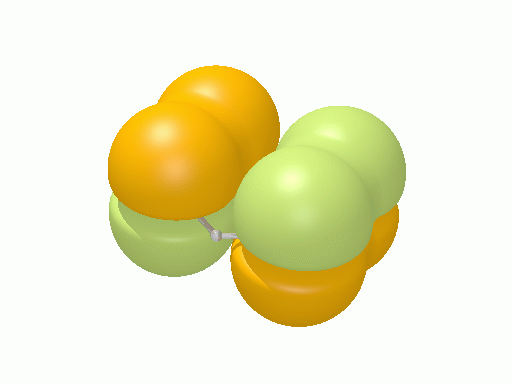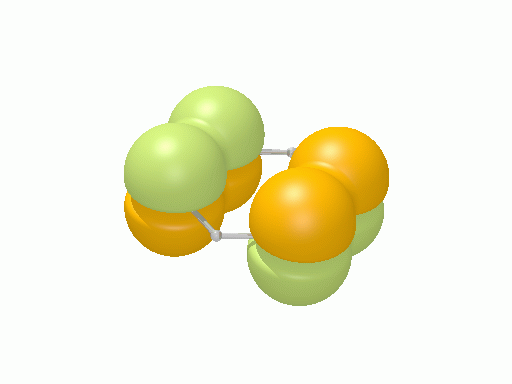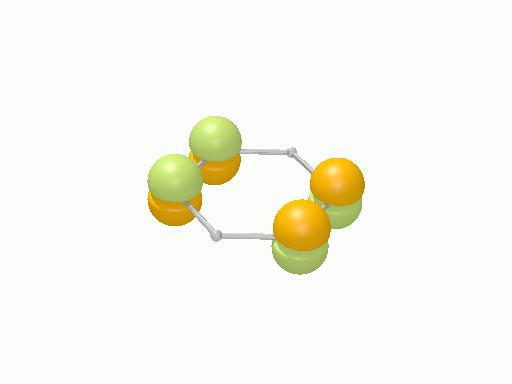
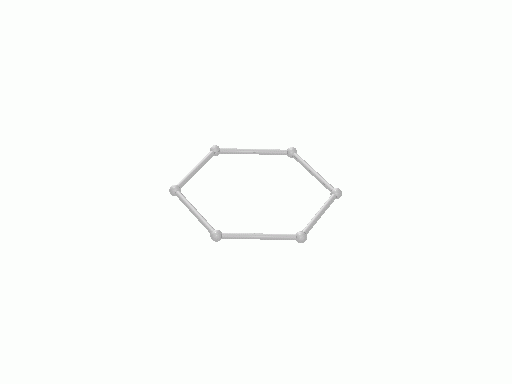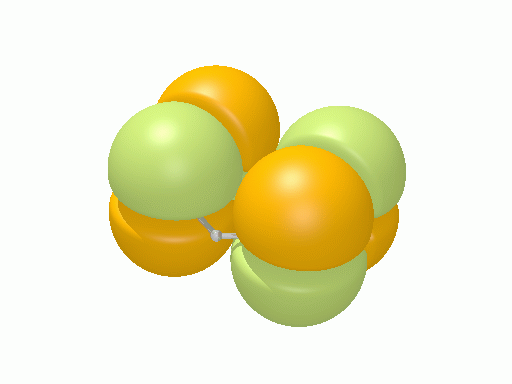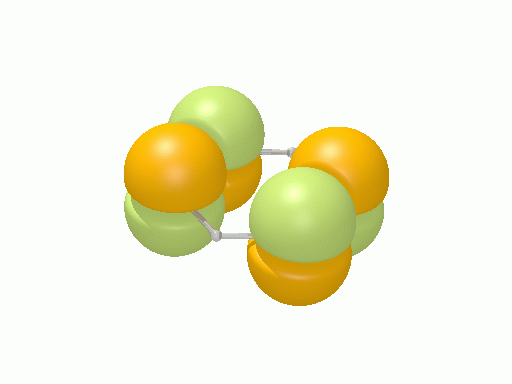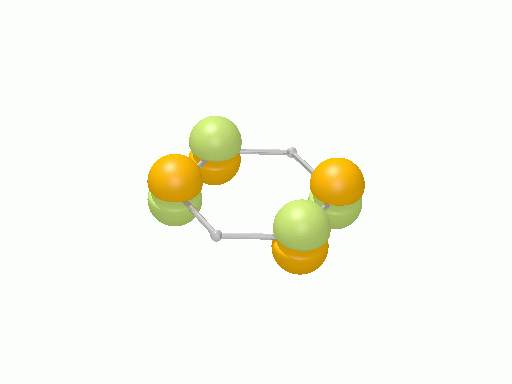
以下の図は波動関数の実部、

$Re[\Psi(r,t)]=Re[\psi(r)\exp\(-i\frac{E}{\hbar}t\)]$

を等値面で描いたものである。軌道関数が実数なら波動関数は定在波となり、複素数ならば回転するように見える。なお軌道エネルギーが高いほど振動の周期が短くなるが、下図では簡単のためすべて同一の振動数にしてある。

エチレン †

アリル †

シクロプロペニル †

ベンゼン †

波動関数の実数化 †

形が同一で互いに逆回転している波動関数は、共役複素数の関係にある。縮退した軌道関数はどんな線形接合をとってもシュレーディンガー方程式を満たすので、複素軌道関数を足したり引いたりすることによって実関数にすることができる。たとえば、a(r), b(r)を実関数として

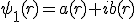
$\psi_1(r)=a(r)+ib(r)$

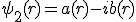
$\psi_2(r)=a(r)-ib(r)$

と表されるならば、

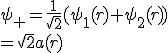
$\psi_+=\frac1{\sqrt2}(\psi_1(r)+\psi_2(r))\\=\sqrt2a(r)$

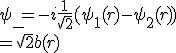
$\psi_-=-i\frac1{\sqrt2}(\psi_1(r)-\psi_2(r))\\=\sqrt2b(r)$

という新しい軌道関数を作ることができる。以下の図はシクロプロペニルとベンゼンのπ分子軌道をすべて実数化したものである。

シクロプロペニル †

ベンゼン †

※図の著作権は北條博彦に属します。教育目的で使用を希望される場合はメールでご一報いただければ幸いです（ポップアップがブロックされる場合はCtlを押しながらクリック）。

Topに戻る